9. 排序算法 - java实现
本文共 15174 字,大约阅读时间需要 50 分钟。
文章目录
1. 基本概念说明
1.1 术语说明
- 稳定:a=b, a在b前面,排序后a仍然在b前面。
- 不稳定:a=b,a在b前面,排序后a可能在b前面,也可能在b后面。
- 内排序:需要排序的数据全部放在内存中。
- 外排序:数据太大,内存放不下,有一部分保存在外存中。
1.2 各种排序算法的复杂度
| 排序算法 | 平均情况 | 最好情况 | 最差情况 | 辅助空间 | 稳定性 |
|---|---|---|---|---|---|
| 冒泡排序 | O ( n 2 ) O(n^2) O(n2) | O ( n ) O(n) O(n) | O ( n 2 ) O(n^2) O(n2) | O ( 1 ) O(1) O(1) | 稳定 |
| 快速排序 | O ( n l o g n ) O(nlogn) O(nlogn) | O ( n l o g n ) O(nlogn) O(nlogn) | O ( n 2 ) O(n^2) O(n2) | O ( l o g n ) − O ( n ) O(logn)-O(n) O(logn)−O(n) | 不稳定 |
| 简单选择排序 | O ( n 2 ) O(n^2) O(n2) | O ( n 2 ) O(n^2) O(n2) | O ( n 2 ) O(n^2) O(n2) | O ( 1 ) O(1) O(1) | 稳定 |
| 堆排序 | O ( n l o g n ) O(nlogn) O(nlogn) | O ( n l o g n ) O(nlogn) O(nlogn) | O ( n l o g n ) O(nlogn) O(nlogn) | O ( 1 ) O(1) O(1) | 不稳定 |
| 直接插入排序 | O ( n 2 ) O(n^2) O(n2) | O ( n ) O(n) O(n) | O ( n 2 ) O(n^2) O(n2) | O ( 1 ) O(1) O(1) | 稳定 |
| 希尔排序 | O ( n l o g n ) − O ( n 2 ) O(nlogn)-O(n^2) O(nlogn)−O(n2) | O ( n l o g n ) O(nlogn) O(nlogn) | O ( n 2 ) O(n^2) O(n2) | O ( 1 ) O(1) O(1) | 不稳定 |
| 归并排序 | O ( n l o g n ) O(nlogn) O(nlogn) | O ( n l o g n ) O(nlogn) O(nlogn) | O ( n l o g n ) O(nlogn) O(nlogn) | O ( n ) O(n) O(n) | 稳定 |
1.3 应用到的基本方法
/** * @Description: 交换下标i和j元素的值 * @param array * @param i * @param j */ public static void swap(int[] array, int i, int j) { int temp = array[i]; array[i] = array[j]; array[j] = temp; } /** * @Description: 打印数组array * @param array */ public static void print(int[] array) { for (int i : array) { System.out.print(i + ","); } System.out.println(" "); } 2. 冒泡排序
2.1 基本描述
属于比较交换排序,基本思想是将小数或大数从底部排到顶部,类似冒泡。
2.2 图解

2.3 实现代码
public static int[] bubbleSort(int[] array) { if (array == null) { throw new NullPointerException("array is null!"); } for (int i = 0; i < array.length; i++) { for (int j = 0; j < array.length - 1 - i; j++) { if (array[j] > array[j + 1]) { swap(array, j, j + 1); } } } return array; } public static int[] bubbleSort2(int[] array) { if (array == null) { throw new NullPointerException("array is null!"); } for (int i = 0; i < array.length; i++) { for (int j = array.length - 1; j > i; j--) { if (array[j] < array[j - 1]) { swap(array, j, j - 1); } } } return array; } 2.4 改进方法
public static int[] bubbleSort1(int[] array) { if (array == null) { throw new NullPointerException("array is null!"); } boolean flag = true; // 如果没有交换,则表明接下来的数据都是有序的,退出循环 for (int i = 0; i < array.length && flag; i++) { flag = false; for (int j = 0; j < array.length - 1 - i; j++) { if (array[j] > array[j + 1]) { swap(array, j, j + 1); flag = true; } } } return array; } 3. 快速排序
3.1 基本描述
- 对冒泡排序的改进,增大了数据比较和移动的距离,将较大的数直接移到后面,较小的数直接移到前面,从而减少总的比较和移动次数。
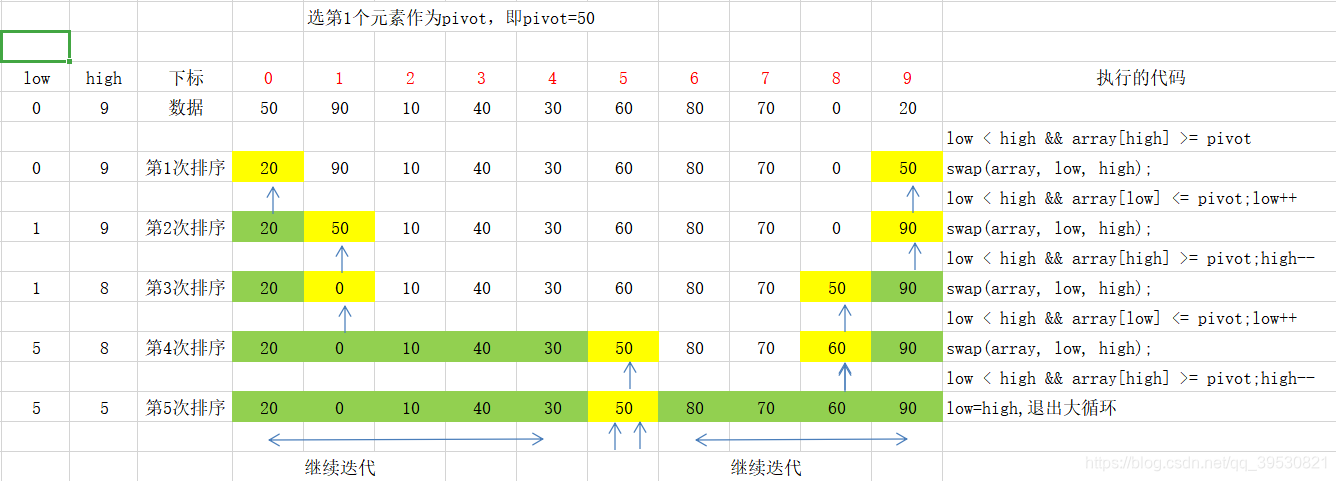
- 运用分治思想,把一个串list变成两个子串sub-list,选定一个基准值pivot,所有比pivot小的数移到较小的列,所有比pivot大的数移到较大的列。
3.2 图解1

3.3 图解2
3.4 实现代码
public static int[] quickSort(int[] array, int low, int high) { if (array == null) { throw new NullPointerException("array is null!"); } if (low < high) { int pivotIndex = partition(array, low, high); quickSort(array, low, pivotIndex - 1); quickSort(array, pivotIndex + 1, high); } return array; } public static int partition(int[] array, int low, int high) { int pivot = array[low]; while (low < high) { while (low < high && array[high] >= pivot) { high--; } swap(array, low, high); while (low < high && array[low] <= pivot) { low++; } swap(array, low, high); } return low; } 3.5 快速排序优化
3.5.1 基准值pivot的优化
固定取第一个作为基准值pivot(其实无论固定取哪一个都一样)是性能的瓶颈,因为这个数很有可能是比较大或者比较小的数,合理选择是pivot尽量靠近中间值。有人提出三数取中法:取数列左中右三个数(也可以随机取),然后排序,取排序后中间的数。
partition方法改造后的代码:public static int partition(int[] array, int low, int high) { int mid = low + (high - low) / 2; // 交换后左端比较小 if (array[low] > array[high]) { swap(array, low, high); } // 交换后保证最大值在右边 if (array[mid] > array[high]) { swap(array, mid, high); } // 交换后保证中间值在左边 if (array[mid] > array[low]) { swap(array, low, mid); } int pivot = array[low]; // 取第1位作为pivot, while (low < high) { while (low < high && array[high] >= pivot) { high--; } swap(array, low, high); while (low < high && array[low] <= pivot) { low++; } swap(array, low, high); } return low; } 3.5.2 优化不必要的交换
观察50的下标变化,从0->9->1->8->5,最后的位置是5,可以采用替换。
public static int partition(int[] array, int low, int high) { int mid = low + (high - low) / 2; // 交换后左端比较小 if (array[low] > array[high]) { swap(array, low, high); } // 交换后保证最大值在右边 if (array[mid] > array[high]) { swap(array, mid, high); } // 交换后保证中间值在左边 if (array[mid] > array[low]) { swap(array, low, mid); } int pivot = array[low]; // 取第1个位pivot while (low < high) { while (low < high && array[high] >= pivot) { high--; } // swap(array, low, high); array[low] = array[high];// 采用替换的操作,而不是交换 while (low < high && array[low] <= pivot) { low++; } // swap(array, low, high); array[high] = array[low];// 采用替换的操作,而不是交换 } array[low] = pivot; return low; } 3.5.3 优化小数组的方案
快速排序运用到递归,对于大数组而言,影响不大,但是对于小数组,简单插入排序性能更好。
public static int[] quickSort(int[] array, int low, int high) { if (array == null) { throw new NullPointerException("array is null!"); } if (high - low > MAX_LENGTH_INSERTION_SORT) { // 有人认为7,有人认为50 int pivotIndex = partition(array, low, high); quickSort(array, low, pivotIndex - 1); quickSort(array, pivotIndex + 1, high); } else { insertionSort(array, low, high); } return array; } 3.5.4 优化递归操作
递归耗用栈,quickSort尾部有两次递归,如果待排序的序列划分极端不平衡,递归深度趋近与n,而不是 log 2 n \log_2{n} log2n。
public static int[] quickSort1(int[] array, int low, int high) { if (array == null) { throw new NullPointerException("array is null!"); } if (high - low > MAX_LENGTH_INSERTION_SORT) { // 有人认为7,有人认为50 while (low < high) { int pivotIndex = partition(array, low, high); quickSort1(array, low, pivotIndex - 1); low = pivotIndex + 1; } } else { insertionSort(array, low, high); } return array; } 第一次递归后,low就没用,此时low = pivot + 1,再来一次循环做partition,效果等同于quickSort(array,pivot +1 ,high)。
3.7 最终代码
public class QuickSort { // 有人认为7比较合适,也有人认为50比较合适 private static final int MAX_LENGTH_INSERTION_SORT = 7; public static void main(String[] args) { int[] array = { 9, 5, 1, 4, 3, 6, 8, 7, 0, 2, 55, 86, 5 }; quickSort1(array, 0, array.length - 1); print(array); } public static int[] quickSort(int[] array, int low, int high) { if (array == null) { throw new NullPointerException("array is null!"); } if (high - low > MAX_LENGTH_INSERTION_SORT) { // 有人认为7,有人认为50 int pivotIndex = partition(array, low, high); quickSort(array, low, pivotIndex - 1); quickSort(array, pivotIndex + 1, high); } else { insertionSort(array, low, high); } return array; } public static int[] quickSort1(int[] array, int low, int high) { if (array == null) { throw new NullPointerException("array is null!"); } if (high - low > MAX_LENGTH_INSERTION_SORT) { // 有人认为7,有人认为50 while (low < high) { int pivotIndex = partition(array, low, high); quickSort1(array, low, pivotIndex - 1); low = pivotIndex + 1; } } else { insertionSort(array, low, high); } return array; } public static int partition(int[] array, int low, int high) { int mid = low + (high - low) / 2; // 交换后左端比较小 if (array[low] > array[high]) { swap(array, low, high); } // 交换后保证最大值在右边 if (array[mid] > array[high]) { swap(array, mid, high); } // 交换后保证中间值在首位 if (array[mid] > array[low]) { swap(array, low, mid); } int pivot = array[low]; // 取第一个值,保存基准值 while (low < high) { while (low < high && array[high] >= pivot) { high--; } // swap(array, low, high); array[low] = array[high];// 采用替换的操作,而不是交换 while (low < high && array[low] <= pivot) { low++; } // swap(array, low, high); array[high] = array[low];// 采用替换的操作,而不是交换 } array[low] = pivot; return low; } public static int[] insertionSort(int[] array, int low, int high) { // 第1个元素默认为单个元素的有序数组 int length = high + 1; for (int i = low + 1; i < length; i++) { for (int j = i; j > low; j--) { if (array[j] < array[j - 1]) { swap(array, j, j - 1); } } } return array; } public static void swap(int[] array, int i, int j) { int temp = array[i]; array[i] = array[j]; array[j] = temp; } public static void print(int[] array) { for (int i : array) { System.err.print(i + ","); } System.out.println(" "); }} 4. 简单选择排序
4.1 基本描述
从n个数中,选出最小的值放在第1个位置;在n-1个数中,选出最小的值放在第2个位置,以此类推。
4.2 图解

4.3 实现代码
public static int[] selectionSort(int[] array) { if (array == null) { throw new NullPointerException("array is null!"); } int minIndex ; for (int i = 0; i < array.length; i++) { minIndex = i; for (int j = i+1; j < array.length; j++) { if (array[j] < array[minIndex]) { minIndex = j; } } if (i != minIndex) { swap(array, minIndex, i); } } return array; } 5. 堆排序
5.1 什么是堆
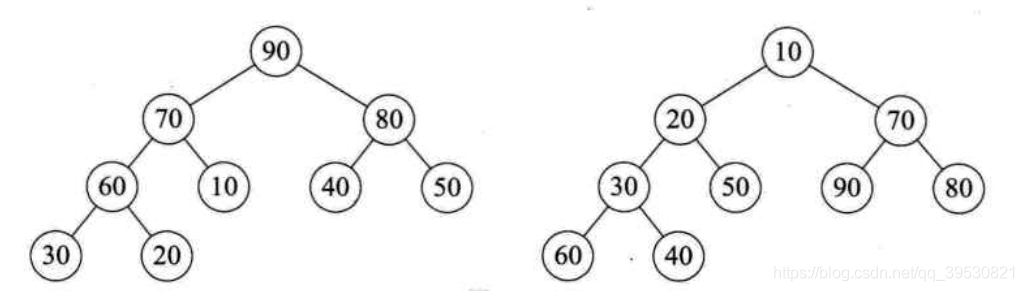
- 堆是****;
- 每个节点都大于或等于其左右孩子的堆,称为大顶堆;
- 每个节点都小于或等于其左右孩子的堆,称为小顶堆。 下面左图为大顶堆,右图是小顶堆。
5.2 涉及的完全二叉树的性质
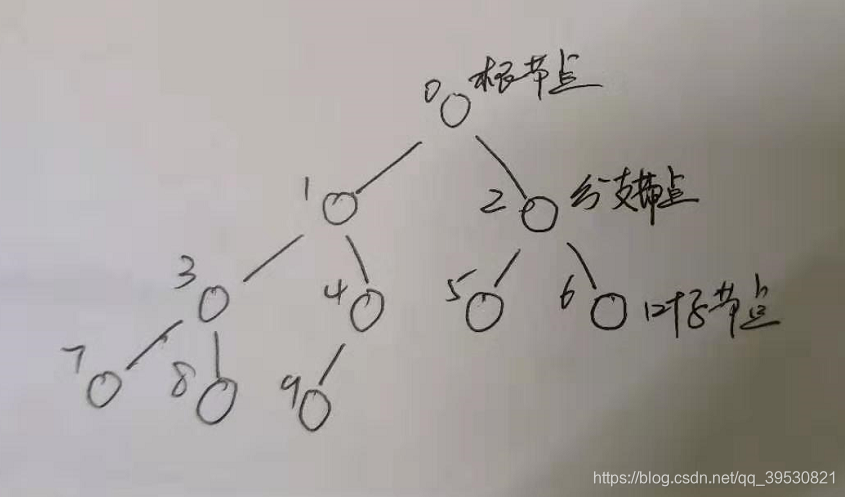
- i=0时,则为根节点;
- 父节点与左孩子的关系: 2 ∗ i + 1 2 * i+1 2∗i+1;
- 父节点与右孩子的关系: 2 ∗ i + 2 2 * i+2 2∗i+2。
5.3 基本思想
- 将初始待排序关键字序列(R1,R2….Rn)构建成大顶堆,此堆为初始的无序区;
- 将堆顶元素R[1]与最后一个元素R[n]交换,此时得到新的无序区(R1,R2,……Rn-1)和新的有序区(Rn),且满足R[1,2…n-1]<=R[n];
- 由于交换后新的堆顶R[1]可能违反堆的性质,因此需要对当前无序区(R1,R2,……Rn-1)调整为新堆,然后再次将R[1]与无序区最后一个元素交换,得到新的无序区(R1,R2….Rn-2)和新的有序区(Rn-1,Rn)。不断重复此过程直到有序区的元素个数为n-1,则整个排序过程完成。
5.4 动图

5.5 实现代码
public class HeapSort { public static void main(String[] args) { int[] array = { 50, 10, 90, 30, 70, 40, 80, 60, 20 }; heapSort2(array); print(array); } public static int[] heapSort(int[] array) { int length = array.length; // 从下标最大的父节点开始做调整,直到形成大顶堆 for (int i = length / 2 - 1; i >= 0; i--) { heapAdjust(array, i, length); } for (int i = length - 1; i >= 0; i--) { swap(array, 0, i); heapAdjust(array, 0, i); } return array; } /** * @Description: 调整堆,将较大的值调整到父节点 * @param array 数组 * @param s 开始下标 * @param size 调整堆 * @return */ public static void heapAdjust(int[] array, int s, int size) { int temp = array[s]; for (int j = 2 * s + 1; j < size; j = 2 * j + 1) { // 左孩子小于右孩子,j加1,此时j是右孩子 if (j < (size - 1) && array[j] < array[j + 1]) { ++j; } // 如果父节点大于等于左右孩子,停止调整 if (temp >= array[j]) { break; } // 执行到这,说明父节点小于孩子,调整 array[s] = array[j]; // 开始下标的调整,继续下个循环 s = j; } array[s] = temp; } public static int[] heapSort2(int[] array) { int length = array.length; // 从下标最大的父节点开始做调整,直到形成大顶堆 for (int i = length / 2 - 1; i >= 0; i--) { heapAdjust2(array, i, length); } for (int i = length - 1; i >= 0; i--) { swap(array, 0, i); heapAdjust2(array, 0, i); } return array; } public static void heapAdjust2(int[] array, int s, int size) { int maxIndex = s; // 如果有左孩子,左孩子大于父节点,将最大指针指向左孩子 if (s * 2 + 1 < size && array[s * 2 + 1] > array[maxIndex]) { maxIndex = s * 2 + 1; } // 如果有右孩子,右孩子大于父节点,将最大指针指向右孩子 if (s * 2 + 2 < size && array[s * 2 + 2] > array[maxIndex]) { maxIndex = s * 2 + 2; } // 如果父节点不是最大,交换父节点与最大值,并且递归 if (maxIndex != s) { swap(array, s, maxIndex); heapAdjust2(array, maxIndex, size); } } public static void swap(int[] array, int i, int j) { int temp = array[i]; array[i] = array[j]; array[j] = temp; } public static void print(int[] array) { for (int i : array) { System.out.print(i + ","); } System.out.println(" "); }} 6. 直接插入排序
6.1 基本描述
稳定的算法,基本思想是将数列分为有序(可将首元素看做是一个有序的数列)和无序两个子列,将无序子列数据在有序子列找到相应位置,插入即可。比简单选择和冒泡的性能要好一些。
6.2 图解

6.3 实现代码
public static int[] insertionSort(int[] array) { if (array == null) { throw new NullPointerException("array is null!"); } // 第1个元素默认为单个元素的有序数组 for (int i = 1; i < array.length; i++) { for (int j = i; j > 0; j--) { if (array[j] < array[j - 1]) { swap(array, j, j - 1); } } } return array; } public static int[] insertionSort1(int[] array) { if (array == null) { throw new NullPointerException("array is null!"); } // 第1个元素默认为单个元素的有序数组 for (int i = 1; i < array.length; i++) { int temp = array[i]; int preIndex = i - 1; while (preIndex >= 0 && array[preIndex] > temp) { array[preIndex + 1] = array[preIndex]; preIndex--; } array[preIndex + 1] = temp; } return array; } 7. 希尔排序
7.1 基本描述
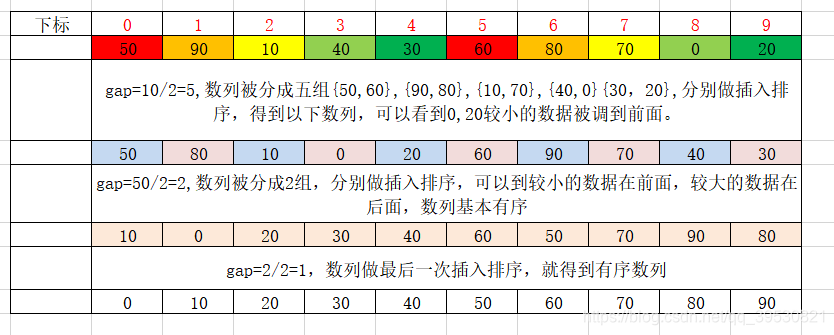
希尔排序是把记录按下标的一定增量分组,对每组使用直接插入排序算法排序;随着增量逐渐减少,每组包含的记录越来越多,当增量减至1时,整个数列恰被分成一组,算法便终止。
7.2 图解

7.3 实现代码
public static int[] shellSort(int[] array) { if (array == null) { throw new NullPointerException("array is null!"); } int gap = array.length / 2; while (gap > 0) { for (int i = gap; i < array.length; i++) { for (int j = i; j > gap - 1; j -= gap) { if (array[j] < array[j - gap]) { swap(array, j, j - gap); } } } gap /= 2; } return array; } public static int[] shellSort1(int[] array) { if (array == null) { throw new NullPointerException("array is null!"); } int gap = array.length / 2; while (gap > 0) { for (int i = gap; i < array.length; i++) { int temp = array[i]; int preIndex = i - gap; while (preIndex >= 0 && array[preIndex] > temp) { array[preIndex + gap] = array[preIndex]; preIndex -= gap; } array[preIndex + gap] = temp; } gap /= 2; } return array; } 7.4 优化点
增量gap的选取是个关键,目前没有找到最好的增量序列。
参考:https://blog.csdn.net/Foliciatarier/article/details/538911448. 归并排序
8.1 基本描述
性能不受输入数据的影响,始终是 O ( n l o g n ) O(nlogn) O(nlogn),代价是需要额外的空间。
归并排序采用分治的思想。 归并:将已有序的子序列合并,得到完全有序的序列;即先使每个子序列有序,再使子序列段间有序。若将两个有序表合并成一个有序表,称为2-路归并。8.2 图解

8.3 实现代码
public class MergeSort { public static void main(String[] args) { int[] array = { 9, 5, 1, 4, 3, 6, 8, 7, 0, 2 }; int[] result = mergeSort(array); print(result); } public static int[] mergeSort(int[] array) { if (array == null) { throw new NullPointerException("array is null!"); } if (array.length < 2) { return array; } int mid = array.length / 2; int[] left = Arrays.copyOfRange(array, 0, mid); int[] right = Arrays.copyOfRange(array, mid, array.length); return merge(mergeSort(left), mergeSort(right)); } public static int[] merge(int[] left, int[] right) { int leftLength = left.length; int rightLength = right.length; int[] result = new int[leftLength + rightLength]; int resultLength = result.length; for (int index = 0, leftIndex = 0, rightIndex = 0; index < resultLength; index++) { if (leftIndex >= leftLength) { // 说明左列已经合并完 result[index] = right[rightIndex++]; } else if (rightIndex >= rightLength) { // 说明右列已经合并完 result[index] = left[leftIndex++]; } else if (left[leftIndex] > right[rightIndex]) { // 说明左列的数值比右列的大,则合并右列的值 result[index] = right[rightIndex++]; } else { result[index] = left[leftIndex++]; } } return result; } public static void swap(int[] array, int i, int j) { int temp = array[i]; array[i] = array[j]; array[j] = temp; } public static void print(int[] array) { for (int i : array) { System.out.print(i + ","); } System.out.println(" "); }} 参考:
- 大话数据结构
- https://www.cnblogs.com/guoyaohua/p/8600214.html
- https://www.runoob.com/w3cnote/bubble-sort.html
- https://juejin.im/post/5bf9f2285188256b0f5832a0
你可能感兴趣的文章